Espacios vectoriales

Mientras que la unidad básica de información en la computación cuántica es el qubit, el escenario en el que tiene lugar el cómputo cuántico es una abstracción matemática llamada espacio vectorial. Resulta que los estados cuánticos se comportan matemáticamente de forma análoga a los vectores físicos. Este tipo de espacio comparte con los vectores físicos las propiedades más fundamentales que éstos poseen, por ejemplo, una “longitud”. En esta sección vamos a examinar más en general los vectores de estado y hablar un poco sobre los espacios que habitan.

Un espacio vectorial $V$ es un conjunto no vacío con elementos $u$ , $v$ llamados vectores, para los cuales están definidas las dos operaciones siguientes:

Suma de vectores: Dadas dos vectores 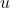$u$ y $v$ en un espacio vectorial $V$ , su suma $w = u + v$ es también un elemento de $V$ . Es decir, al sumar dos vectores del espacio, el resultado sigue siendo un vector del mismo espacio.
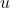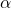Multiplicación por un escalar: Dados un vector $u$ en el espacio vectorial $V$ y un número (escalar) $\alpha$ , el producto 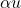$\alpha u$ también pertenece a $V$ . Es decir, al multiplicar un vector por un escalar, el resultado sigue siendo un vector del mismo espacio.

Además, en el espacio vectorial $V$ se cumplen los siguientes axiomas:

Axioma 1. Asociatividad de la suma. $(u+v)+w=u+(v+w)$

Axioma 2. Existencia del vector cero.
Existe un vector 0 que pertence a $V$ tal que $u + 0 = 0 + u = u$

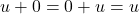
Axioma 3. Existencia del inverso aditivo.
Para cada $u\in V$ existe un $-u\in V$ (vector opuesto) que cumple: $u+(−u)=(−u)+u=0$

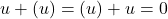
Axioma 4. Conmutatividad de la suma.
Para todo $u, v\in V$ se cumple que $u + v = v + u$

Un espacio vectorial fundamental en computación cuántica es $\mathbb{C}^n$ , el espacio de las “n-uplas” de números complejos. “N-upla” solo significa una colección ordenada de $n$ números. Siguiendo la notación de los qubits, etiquetamos los elementos de $\mathbb{C}^n$ como $\ket{a}, \ket{b}, \ket{c}$ , etc.

Un elemento genérico de este espacio se puede representar como un vector columna de dimensión $n$ , es decir, la lista ordenada de sus componentes $a_1, a_2, \dots, a_n$ :

$\ket{a} = \begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n\end{pmatrix}$

Este tipo de notación puede usarse también para qubits. Retomando la forma general de la ecuación de $\psi$ , o sea $\ket{\psi} = \alpha\ket{0} + \beta\ket{1}$ , lo escribimos como vector columna poniendo el coeficiente de $\ket{0}$ en la primera fila y el de $\ket{1}$ en la segunda:

$\ket{\psi} = \begin{pmatrix} \alpha \\ \beta \end{pmatrix}$

Por ejemplo si tenemos que el siguiente qubit $\ket{\psi} = \frac{1}{\sqrt{5}} \ket{0} + \frac{2}{\sqrt{5}} \ket{1}$ , su representación como vector columna es

$\ket{\psi} = \begin{pmatrix} \frac{1}{\sqrt{5}} \\ \frac{2}{\sqrt{5}} \end{pmatrix} = \frac{1}{\sqrt{5}} \begin{pmatrix} 1 \\ 2 \end{pmatrix}$

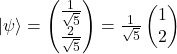
La multiplicación de un vector por un escalar se realiza como sigue:

$\alpha \ket{a} = \alpha \begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix} = \begin{pmatrix} \alpha a_1 \\ \alpha a_2 \\ \vdots \\ \alpha a_n \end{pmatrix}$

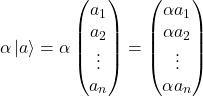
Esta multiplicación por escalar produce un vector con $n$ números complejos por tanto podemos ver que $\mathbb{C}^n$ está cerrado bajo la multiplicación por escalares.

El vector suma se hace sumando componente a componente:

$\ket{a} + \ket{b} = \begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix} + \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{pmatrix} = \begin{pmatrix} a_1 + b_1 \\ a_2 + b_2 \\ \vdots \\ a_n + b_n \end{pmatrix}$

Entradas Relacionadas