Podemos introducir una unidad elemental de procesamiento de información propia de la computación cuántica: el qubit (abreviatura de quantum bit, o bit cuántico). Aunque a primera vista recuerda al bit clásico, pronto descubriremos que su naturaleza es muy distinta y que esa diferencia nos brinda maneras completamente nuevas e interesantes de manejar la información.
Como el bit, el qubit posee dos “niveles” básicos, que etiquetamos como ![]() y
y ![]() . Sin embargo, a diferencia de un bit convencional que sólo puede estar en uno u otro, el qubit también puede hallarse en una superposición de ambos estados. Denotando su estado genérico por
. Sin embargo, a diferencia de un bit convencional que sólo puede estar en uno u otro, el qubit también puede hallarse en una superposición de ambos estados. Denotando su estado genérico por ![]() , esa superposición se expresa matemáticamente como una combinación lineal de
, esa superposición se expresa matemáticamente como una combinación lineal de ![]() y
y ![]() . O sea
. O sea
![]()
Aquí, ![]() y
y ![]() son números complejos
son números complejos ![]() , con
, con ![]() .
.
Mientras un qubit pueda existir en una superposición de los estados ![]() y
y ![]() , al medirlo siempre colapsa a uno de ellos. Las leyes de la mecánica cuántica nos dice que si
, al medirlo siempre colapsa a uno de ellos. Las leyes de la mecánica cuántica nos dice que si ![]() , entonces:
, entonces:
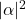 es la probalidad de encontrar
es la probalidad de encontrar 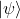 en
en 
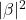 es la probalidad de encontrar
es la probalidad de encontrar 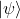 en
en 
Y, como la suma de las probabilidades tiene que ser 1, estos coeficientes ![]() y
y ![]() tienen que cumplir
tienen que cumplir ![]() .
.
En terminos generales si un evento tiene ![]() posibles resultados y etiquetamos la probabilidad de obtener el resultado
posibles resultados y etiquetamos la probabilidad de obtener el resultado ![]() como
como ![]() , la condición de que las probabilidades sumen 1 es:
, la condición de que las probabilidades sumen 1 es:

Cuando los cuadrados de los coeficientes del qubit satisfacen la ecuación anterior, decimos que el qubit está normalizado. Para calcular el módulo de cada coeficiente (recordando que son números complejos)
![]()
![]()
donde ![]() es el conjugado complejo de
es el conjugado complejo de ![]() y
y ![]() es el conjugado complejo de
es el conjugado complejo de ![]() . Recordamos que el conjugado complejo de un número complejo
. Recordamos que el conjugado complejo de un número complejo ![]() lo obtenemos cambiano de signo la parte imaginaria, o sea si
lo obtenemos cambiano de signo la parte imaginaria, o sea si ![]() entonces
entonces ![]() . Entonces para ir terminando calculamos el módulo de
. Entonces para ir terminando calculamos el módulo de ![]() como:
como:
![]()
![]()